461. 汉明距离

[力扣原题链接](https://leetcode-cn.com/problems/hamming-distance/)

## 题目

两个整数之间的==汉明距离==指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数`x`和`y`，计算它们之间的汉明距离。

注意：`0 ≤ x, y < 231.`

**示例 1:**

```
输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。
```
## 思路

循环计算`x`，`y`的二进制，统计二进制位不同的位置的数目。

## 代码

语言：Java

```
class Solution {
    public int hammingDistance(int x, int y) {
        int result = 0;
        while((x != 0) || (y != 0)){
            int xTmp = x % 2;
            int yTmp = y % 2;
            if(xTmp != yTmp) {
                result++;
            }
            x /= 2;
            y /= 2;
        }
        return result;
    }
}
```

## 力扣官方代码
**思路**
汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。
根据以上定义，我们使用异或运算，记为 `⊕`，当且仅当输入位不同时输出为`11`。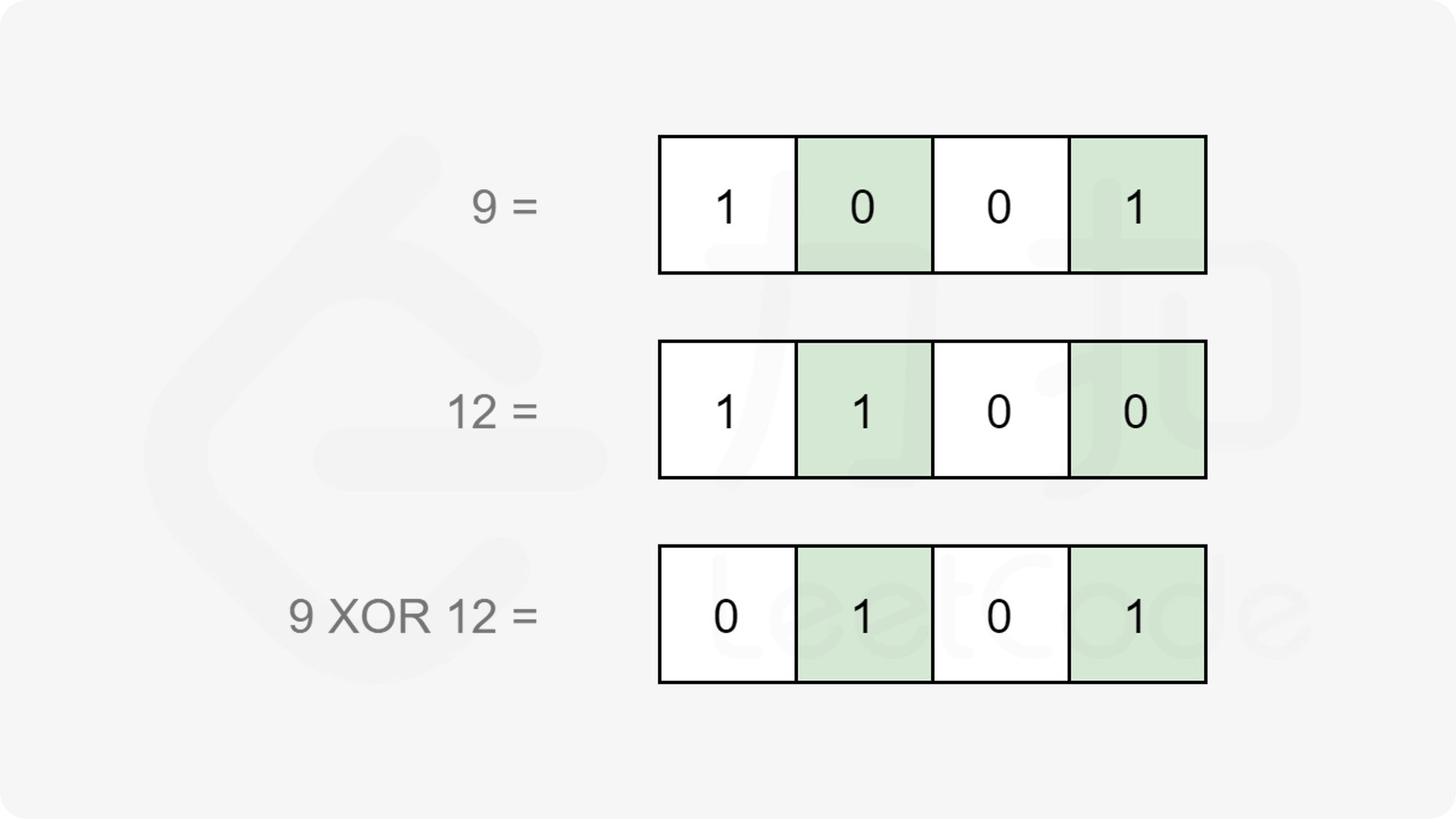

![](/media/202105/2021-05-27_094824.png)

计算 `x`和 `y`之间的汉明距离，可以先计算`x⊕y`，然后统计结果中等于`11`的位数。

现在，原始问题转换为位计数问题。

**代码**

**方法一：内置位计数功能**
```
class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y);
    }
}
```

**方法二：移位实现位计数**
```
class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            ret += s & 1;
            s >>= 1;
        }
        return ret;
    }
}
```

**方法三：Brian Kernighan 算法**
```
class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            s &= s - 1;
            ret++;
        }
        return ret;
    }
}
```