1074. 元素和为目标值的子矩阵数量

# 题目

## 1074. 元素和为目标值的子矩阵数量

[https://leetcode-cn.com/problems/number-of-submatrices-that-sum-to-target/](https://leetcode-cn.com/problems/number-of-submatrices-that-sum-to-target/)

给出矩阵 `matrix` 和目标值 `target`，返回元素总和等于目标值的非空子矩阵的数量。

子矩阵 `x1, y1, x2, y2` 是满足 `x1 <= x <= x2` 且 `y1 <= y <= y2` 的所有单元 `matrix[x][y]` 的集合。

如果 `(x1, y1, x2, y2)` 和 `(x1', y1', x2', y2')` 两个子矩阵中部分坐标不同（如：`x1 != x1'`），那么这两个子矩阵也不同。

**示例 1：**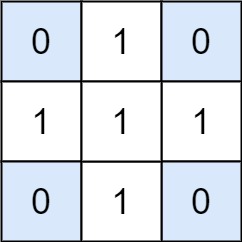

![img](/media/202105/2021-05-30_231244.png)

```
输入：matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出：4
解释：四个只含 0 的 1x1 子矩阵。
```

**示例 2：**

```
输入：matrix = [[1,-1],[-1,1]], target = 0
输出：5
解释：两个 1x2 子矩阵，加上两个 2x1 子矩阵，再加上一个 2x2 子矩阵。
```

**示例 3：**

```
输入：matrix = [[904]], target = 0
输出：0
```

**提示：**

- `1 <= matrix.length <= 100`
- `1 <= matrix[0].length <= 100`
- `-1000 <= matrix[i] <= 1000`
- `-10^8 <= target <= 10^8`

# 题解

## 思路

先求每行的前缀和，再计算列的值

## 代码

```javascript
/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {number}
 */
var numSubmatrixSumTarget = function(matrix, target) {
    let m = matrix.length;
    let n = matrix[0].length;
    // 处理数据，改成前缀和
    for(let i = 0; i < m; i++){
        for(let j = 1;j < n; j++){
            matrix[i][j] += matrix[i][j - 1];
        }
    }
    // hash记录前缀和
    let preMap;
    let sum;
    // 结果
    let ans = 0;
    // 从最外层开始，从左往右的大区间
    for(let i = 0; i < n; i++){
        // 单个小区间，列
        for(let j = i; j < n; j++){
            // 初始化集合
            preMap = new Map();
            // 增加0值，也就是能查到第0个前缀，边界值
            preMap.set(0, 1);
            sum = 0;
            for(let k = 0; k < m; k++){
                // 如果大区间是0，也就是第一列的值，没有边界。非0，则减去大区间的上一个，就得到当前的列前缀和
                sum += i === 0 ? matrix[k][j] : matrix[k][j] - matrix[k][i - 1];
                // 如果减去目标值，在区间能找到，加上对应的次数
                ans += preMap.get(sum - target) || 0;
                // 记录当前出现的次数
                preMap.set(sum, (preMap.get(sum) || 0) + 1);
            }
        }
    }
    return ans;
};
```

## 官方

### 方法一：前缀和 + 哈希表

我们枚举子矩阵的上下边界，并计算出该边界内每列的元素和，则原问题转换成了如下一维问题：

> 给定一个整数数组和一个整数 target，计算该数组中子数组和等于 target 的子数组个数。

力扣上已有该问题：[560. 和为K的子数组](https://leetcode-cn.com/problems/subarray-sum-equals-k/)，读者可以参考其[官方题解](https://leetcode-cn.com/problems/subarray-sum-equals-k/solution/he-wei-kde-zi-shu-zu-by-leetcode-solution/)，并掌握使用前缀和+哈希表的线性做法。

对于每列的元素和 sum 的计算，我们在枚举子矩阵上边界 i 时，初始下边界 j 为 i，此时 sum 就是矩阵第 i 行的元素。每次向下延长下边界 j 时，我们可以将矩阵第 j 行的元素累加到 sum 中。

```javascript
var numSubmatrixSumTarget = function(matrix, target) {
    let ans = 0;
    const m = matrix.length, n = matrix[0].length;
    for (let i = 0; i < m; ++i) { // 枚举上边界
        const sum = new Array(n).fill(0);
        for (let j = i; j < m; ++j) { // 枚举下边界
            for (let c = 0; c < n; ++c) {
                sum[c] += matrix[j][c]; // 更新每列的元素和
            }
            ans += subarraySum(sum, target);
        }
    }
    return ans;
}

### 方法二

#### 本题的基石

建议大家可以先做以下两题：
[1.两数之和](https://leetcode-cn.com/problems/two-sum/)
[560. 和为 K 的子数组](https://leetcode-cn.com/problems/subarray-sum-equals-k/)
本题我们主要还是运用前缀和的思想对数组做一些预处理，然后再暴力遍历所有的情况。
核心：`X + Y = target`， 如果 `target - Y` 存在于哈希表中，则说明有一个区间和为 **X** 的区间满足
`X + Y = target`.

---

#### 步骤

步骤 1： 对数组做预处理。这样我们便能在遍历时可以通过常数计算出当前的区间的和是多少。我们只做横向的前缀和预处理是因为我们会在进行纵向遍历用sum来记录当前的区间和。
![Slide1.PNG](/media/202105/2021-05-30_231614.png)
步骤 2： 外层的 k 代表的是大区间，里层的 j 代表的是当前大区间里的小区间，而在里层的 i 则代表的是 j 小区间里的纵向小区间。
![Slide2.PNG](/media/202105/2021-05-30_231614.png)
步骤 3： 每次遍历当前区间将当前区间和加入哈希表，然后遍历下一个区间和，找满足 `target - Y` 条件的区间。
**注意事项：一定要注意我们的哈希表是局部变量！！！也就是说我们的哈希表储存的是区间 `J` 的前缀和，如果不这样做我们会得到错误的区间不满足答案需求** 。

```java
class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size(), ans = 0;
        //前缀和预处理
        for(int i = 0; i < m; ++i)
            for(int j = 1; j < n; ++j)
                matrix[i][j] += matrix[i][j-1];
        
        for(int k = 0; k < n; ++k)
        {
            for(int j = k; j < n; ++j)
            {
                int sum = 0;
                //加入 {0,1} 以0，0为左上角的区间和等于target，属于边界情况
                unordered_map<int, int> mp = {{0,1}};
                for(int i = 0; i < m; ++i)
                {
                    //计算当前区间的区间和
                    sum += (k == 0? matrix[i][j] : matrix[i][j] - matrix[i][k-1]);
                    if(mp.count(sum - target)) ans += mp[sum - target];
                    ++mp[sum];
                }
            }
        }
        return ans;
    }
};
```