leetcode每日一题
7月
1833. 雪糕的最大数量
5801. 消灭怪物的最大数量
1418. 点菜展示表
1711. 大餐计数
5792. 统计平方和三元组的数目
274. H 指数
面试题 10.02. 变位词组
6月
1744. 你能在你最喜欢的那天吃到你最喜欢的糖果吗?
42. 接雨水
206. 反转链表
234. 回文链表
141. 环形链表
474. 一和零
5777. 使数组元素相等的减少操作次数
5776. 判断矩阵经轮转后是否一致
1897. 重新分配字符使所有字符串都相等
752. 打开转盘锁
5781. 删除一个字符串中所有出现的给定子字符串
5789. 你完成的完整对局数
5788. 字符串中的最大奇数
852. 山脉数组的峰顶索引
1894. 找到需要补充粉笔的学生编号
5786. 可移除字符的最大数目
1893. 检查是否区域内所有整数都被覆盖
1899. 合并若干三元组以形成目标三元组
5799. 最美子字符串的数目
5780. 删除一个元素使数组严格递增
5月
342. 4的幂
231. 2 的幂
560. 和为K的子数组
141. 环形链表
1074. 元素和为目标值的子矩阵数量
461. 汉明距离
1190. 反转每对括号间的子串
664. 奇怪的打印机
1787. 使所有区间的异或结果为零(放弃治疗)
1707. 与数组中元素的最大异或值
810. 黑板异或游戏
1035. 不相交的线
692. 前K个高频单词
1738. 找出第 K 大的异或坐标值
993. 二叉树的堂兄弟节点
13. 罗马数字转整数
1442. 形成两个异或相等数组的三元组数目
12. 整数转罗马数字
1269. 停在原地的方案数
1734. 解码异或后的排列
1310. 子数组异或查询
872. 叶子相似的树
vditor使用说明
645. 错误的集合
930. 和相同的二元子数组
5793. 迷宫中离入口最近的出口
5843. 作为子字符串出现在单词中的字符串数目
5832. 构造元素不等于两相邻元素平均值的数组
5851. 找出不同的二进制字符串
5850. 找出数组的最大公约数
5835. 最大方阵和
n个人匹配,两两匹配,匹配多轮
本文档使用 MrDoc 发布
-
+
首页
1442. 形成两个异或相等数组的三元组数目
# 题目 ## 1442. 形成两个异或相等数组的三元组数目 [https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor/](https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor/) 给你一个整数数组 `arr` 。 现需要从数组中取三个下标 `i`、`j` 和 `k` ,其中 `(0 <= i < j <= k < arr.length)` 。 `a` 和 `b` 定义如下: - `a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]` - `b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]` 注意:**^** 表示 **按位异或** 操作。 请返回能够令 `a == b` 成立的三元组 (`i`, `j` , `k`) 的数目。 **示例 1:** ``` 输入:arr = [2,3,1,6,7] 输出:4 解释:满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4) ``` **示例 2:** ``` 输入:arr = [1,1,1,1,1] 输出:10 ``` **示例 3:** ``` 输入:arr = [2,3] 输出:0 ``` **示例 4:** ``` 输入:arr = [1,3,5,7,9] 输出:3 ``` **示例 5:** ``` 输入:arr = [7,11,12,9,5,2,7,17,22] 输出:8 ``` **提示:** - `1 <= arr.length <= 300` - `1 <= arr[i] <= 10^8` # 题解 ## 思路 利用异或的性质,题目要求的是 `a == b`, 也就是`a ^ b = 0` ,可转化为 `arr[i]^arr[i+1]^...^arr[k]==0`,则中间的j无论取什么值都成立,即当 `arr[i]^arr[i+1]^...^arr[k]==0` 成立时,可以取到 k-i 种 ## 代码 ```javascript /** * @param {number[]} arr * @return {number} */ var countTriplets = function(arr) { const length = arr.length; if(length < 2) return 0; // 结果 let ans = 0; // 异或值 let xor; for(let i = 0; i < length - 1; i++){ xor = arr[i]; for(let k = i + 1; k < length; k++){ xor ^= arr[k]; if(!xor){ ans += k-i; } } } return ans; }; ``` ## 官方 ### 什么是异或(对于新手) **异或是一种逻辑运算,对两个数异或的结果实际上是看其两个数的比特值在其比特位上是否相同。** 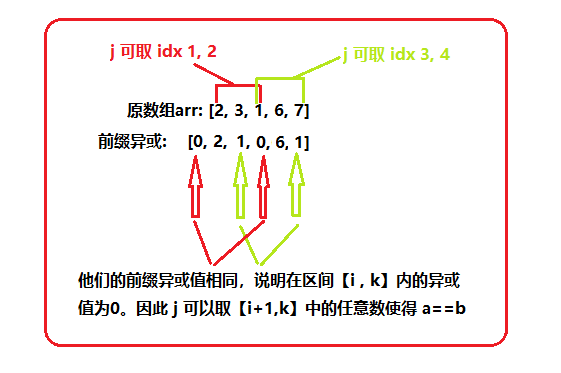 --- ### 由浅到深的思路 **法一: 最直观的暴力法** 我们进行一个三重的循环,然后计算其 arr[i] - arr[j-1]*a**r**r*[*i*]−*a**r**r*[*j*−1] 与 arr[j] - arr[k]*a**r**r*[*j*]−*a**r**r*[*k*] 的异或值,再判断其是否相等。 时间: O(n^4)*O*(*n*4) 空间: O(1)*O*(1) 结果超时,当我们看到44次方的时间复杂度时就知道此法是肯定不可取的,因此我们因该直接放弃暴力解法。 ``` class Solution { public: int countTriplets(vector<int>& arr) { int n = arr.size(), ans = 0; for(int i = 0; i < n; ++i) { for(int j = i+1; j < n; ++j) { for(int k = j; k < n; ++k) { int a = 0, b = 0; for(int x = i; x < j; ++x) a ^= arr[x]; for(int y = j; y <= k; ++y) b ^= arr[y]; ans += (a == b); } } } return ans; } }; ``` --- **法二: 暴力解法的优化(前缀预处理)** a = arr[i] - arr[j-1]*a*=*a**r**r*[*i*]−*a**r**r*[*j*−1] b = arr[j] - arr[k]*b*=*a**r**r*[*j*]−*a**r**r*[*k*] 从法一中我们看到了一个问题,每次计算其 a*a* 与 b*b* 时都需要用两层 loop*l**o**o**p*, 这样的时间消耗是巨大的。那么用什么方法可以避免使用暴力的方法计算区间内的异或值?做预处理,也就是求出其**前缀异或数组**。什么是前缀异或数组?有什么用?(这里cv了以前的题解啊,写过相同的,不想再写一遍...) ``` 异或有自反性: 即任何数异或其本身等于 0; 比如: a ⊕ a = 0; 前缀异或的解释:对于 preXOR[i] 表示为前 i 项数的异或值 假设我们有数组 arr: [1, 2, 3, 4, 7, 9]; 前零项的异或值为: 0 = 0 前一项的异或值为: 1 = 1 前二项的异或值为: 1 ⊕ 2 = 3 前三项的异或值为: 1 ⊕ 2 ⊕ 3 = 0 前四项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 = 4 前五项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 = 3 前六项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9 = 10 因此它的前缀异或数组为 preXOR: [0, 1, 3, 0, 4, 3, 10]; 假设现在我们想求第 3 项到第 6 项的异或值, 此时我们不需要去暴力计算 "3 ⊕ 4 ⊕ 7 ⊕ 9" 我们知道 (3 ⊕ 4 ⊕ 7 ⊕ 9) = (1 ⊕ 2) ⊕ (1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9) 我们可以使用前缀异或的数组来计算第 3 项到第 6 项的异或值 (1 ⊕ 2) 为前 2 项的异或值为 “3” (1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9) 为前 6 项异或值为 “10” 因此第 3 项到第 6 项的异或值为:3 ⊕ 10 = 9 所有对于前缀异或我们同样也可以用O(1)的时间计算区间内的异或值 ```  那么用法一的方法,对于计算其 a*a* 与 b*b*的值我们可以从 O(n)*O*(*n*) 降到 O(1)*O*(1)。结果通过。只要能想到前缀异或数组其实就已经能解决此题了。 时间: O(n^3)*O*(*n*3) 空间: O(n)*O*(*n*), 异或数组所占用的空间 - cpp - python3 ``` class Solution { public: int countTriplets(vector<int>& arr) { int n = arr.size(), ans = 0; vector<int> preXor(n+1); for(int i = 0; i < n; ++i) preXor[i+1] = preXor[i]^arr[i]; for(int i = 1; i <= n; ++i) { for(int j = i+1; j <= n; ++j) { for(int k = j; k <= n; ++k) { int a = preXor[j-1]^preXor[i-1]; int b = preXor[k]^preXor[j-1]; ans += (a == b); } } } return ans; } }; ``` --- **法三: 利用其异或的性质** a = arr[i] - arr[j-1]*a*=*a**r**r*[*i*]−*a**r**r*[*j*−1] b = arr[j] - arr[k]*b*=*a**r**r*[*j*]−*a**r**r*[*k*] 我们知道 `a ⊕ a = 0`的,由于题目让我们找到满足 `a == b` 的坐标,那么当 a*a* 等于 b*b* 时满足什么性质? `a ⊕ b = 0`! 我们就可以得到`arr[i] ^...^ arr[j-1]^ arr[j] ^...^ arr[k] = 0`。**因此在 i\*i\* 之前的前缀异或值到 k\*k\* 时不会变。这是法三的核心!!** 因为【i,k】的区间异或值为0,可以得到: `preXor[i-1] == preXor[k]` 其另一点重点在于在区间 `[i, k]`内 j*j* 在哪并不重要, 因为无论 j*j*在哪,i*i* 到 k*k* 的异或值都等于 0. 不影响结果。  在法二的方法上进一步优化,省去了枚举 j*j* 的步骤。能直接想到这一步的扣友们已经很不错了! 时间: O(n^2)*O*(*n*2) 空间: O(n)*O*(*n*), 异或数组所占用的空间 - cpp - python3 - java ``` class Solution { public: int countTriplets(vector<int>& arr) { int n = arr.size(), ans = 0; vector<int> preXor(n+1); for(int i = 0; i < n; ++i) preXor[i+1] = preXor[i]^arr[i]; for(int i = 1; i <= n; ++i) for(int k = i+1; k <= n; ++k) if(preXor[i-1] == preXor[k]) ans += k-i; return ans; } }; ``` --- **法四:使用哈希表进一步优化时间** 对于法三我们发现我们只在乎其前缀异或值是否出现与其出现的index*i**n**d**e**x*位置。那么我们是否可以用哈希表将其前缀异或值出现得次数记录下来,然后将其每个前缀异或值出现的坐标也记录起来。扣友们直接看代码可能不懂!让我来讲解一番。首先要明白一个事实那就是假设区间 [i, k] 的异或值为 0,那么 j*j* 可以有 `k-i` 种可能性。假设我们遍历到 k*k* 时的前缀异或值为 x*x*, 而前缀异或值 x*x* 在 k*k* 的前面出现了 4 次分别出现在 [i1, i2, i3, i4], 那么 j*j* 有多少种可能性?实际上还是法三,用了数学计算优化! `(k - i1) + (k - i2) + (k - i3) + (k - i4) = 4*k - (i1+i2+i3+i4)` 因此我们得到 `ans += cnt[val]*k - tot[val];` 法四省去了枚举 i*i* 的步骤,因此进一步的优化了时间复杂度。 时间: O(n) 空间:O(n) ``` class Solution { public: int countTriplets(vector<int>& arr) { int n = arr.size(), ans = 0, val = 0; unordered_map<int, int> cnt, tot; for(int k = 0; k < n; ++k) { val ^= arr[k]; ans += cnt[val]*k - tot[val]; //这里不能把 arr[i]包含进去,因为我们需要的是arr[i]前面一项的异或值 //想想法三中的 preXor[i-1] == preXor[k] ++cnt[val^arr[k]]; tot[val^arr[k]] += k; } return ans; } }; ``` --- ### 总结 法二三四其实都运用了前缀异或的思想,本题我们主要需要学习的是异或的性质,以及对于前缀异或理解与运用。只要能想到法三就已经非常不错了,能想到法二也说明对前缀异或有了一定的感觉,对于法四我们当作学习提升所用。希望大家读有所获!
czbiao
2021年5月18日 22:33
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
阅读量
次
本站总访问量
次
本站访客数
人次
Markdown文件
分享
链接
类型
密码
更新密码