474. 一和零

# 题目

## 474. 一和零

[https://leetcode-cn.com/problems/ones-and-zeroes/](https://leetcode-cn.com/problems/ones-and-zeroes/)

给你一个二进制字符串数组 `strs` 和两个整数 `m` 和 `n` 。

请你找出并返回 `strs` 的最大子集的大小，该子集中 **最多** 有 `m` 个 `0` 和 `n` 个 `1` 。

如果 `x` 的所有元素也是 `y` 的元素，集合 `x` 是集合 `y` 的 **子集** 。

**示例 1：**

```
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
```

**示例 2：**

```
输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。
```

**提示：**

- `1 <= strs.length <= 600`
- `1 <= strs[i].length <= 100`
- `strs[i]` 仅由 `'0'` 和 `'1'` 组成
- `1 <= m, n <= 100`

# 题解

## 思路

动态规划，其实就是背包问题

## 代码

```javascript
/**
 * 动态规划
 * @param {string[]} strs
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var findMaxForm = function(strs, m, n) {
    const length = strs.length;
    const dp = new Array(length + 1).fill(0).map(()=>new Array(m + 1).fill(0).map(()=>new Array(n + 1).fill(0)));
    // 0的个数
    let zeros;
    // 1的个数
    let ones;
    for(let i = 1; i <= length; i++) {
        [zeros, ones] = countZeroOne(strs[i - 1]);
        for(let j = 0; j <= m; j++){
            for(let k = 0; k <= n; k++){
                if(j >= zeros && k >= ones){
                    dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - zeros][k - ones] + 1);
                } else {
                    dp[i][j][k] = dp[i - 1][j][k];
                }
            }
        }
    }
    return dp[length][m][n];
};

// 获取0和1的个数
function countZeroOne(str){
    const arr = new Array(2).fill(0);
    for(let s of str) {
        arr[s.charCodeAt() - '0'.charCodeAt()]++;
    };
    return arr;
}
```

## 官方

## 思路

这道题目，还是比较难的，也有点像程序员自己给自己出个脑筋急转弯，程序员何苦为难程序员呢哈哈。

来说题，本题不少同学会认为是多重背包，一些题解也是这么写的。

其实本题并不是多重背包，再来看一下这个图，捋清几种背包的关系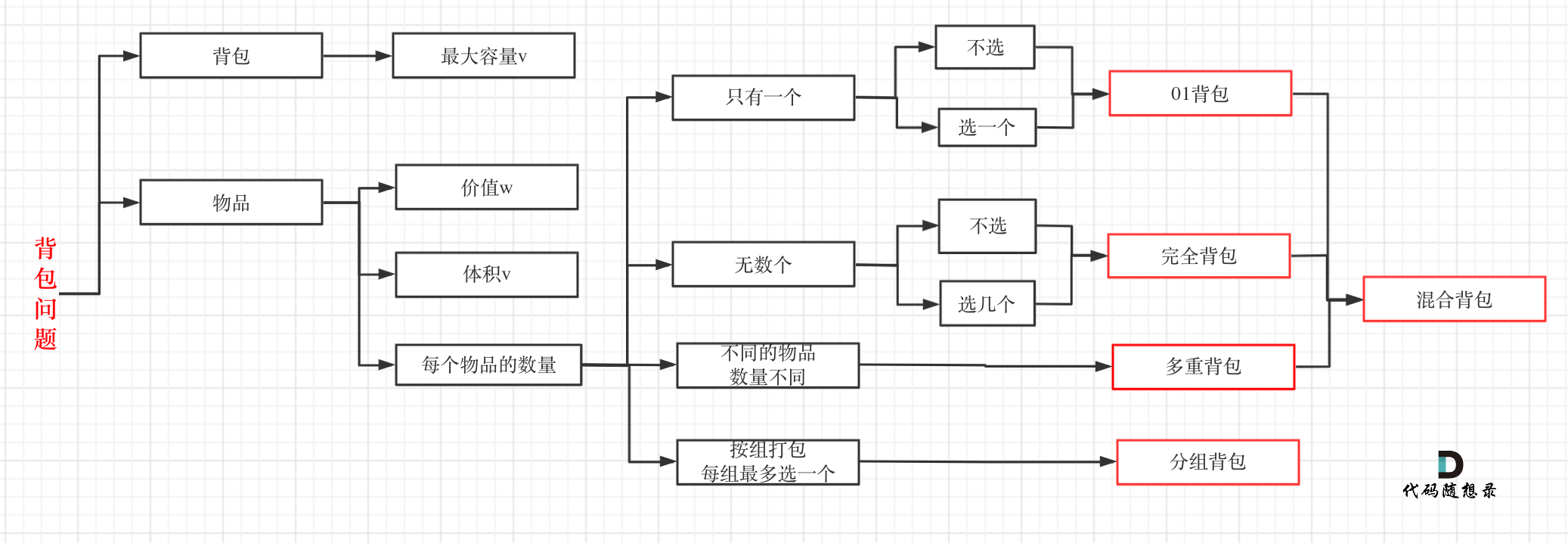

![416.分割等和子集 1](/media/202106/2021-06-06_221406.png)

多重背包是每个物品，数量不同的情况。

**本题中 strs 数组里的元素就是物品，每个物品都是一个！**

**而 m 和 n 相当于是一个背包，两个维度的背包** 。

理解成多重背包的同学主要是把 m 和 n 混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。

但本题其实是 01 背包问题！

这不过这个背包有两个维度，一个是 m 一个是 n，而不同长度的字符串就是不同大小的待装物品。

开始动规五部曲：

1. 确定 dp 数组（dp table）以及下标的含义

**dp[i][j]：最多有 i 个 0 和 j 个 1 的 strs 的最大子集的大小为 dp[i][j]** 。

2. 确定递推公式

dp[i][j] 可以由前一个 strs 里的字符串推导出来，strs 里的字符串有 zeroNum 个 0，oneNum 个 1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取 dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此时大家可以回想一下 01 背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对比一下就会发现，字符串的 zeroNum 和 oneNum 相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

**这就是一个典型的 01 背包！** 只不过物品的重量有了两个维度而已。

3. dp 数组如何初始化

在[动态规划：关于 01 背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)中已经讲解了，01 背包的 dp 数组初始化为 0 就可以。

因为物品价值不会是负数，初始为 0，保证递推的时候 dp[i][j]不会被初始值覆盖。

4. 确定遍历顺序

在[动态规划：关于 01 背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)中，我们讲到了 01 背包为什么一定是外层 for 循环遍历物品，内层 for 循环遍历背包容量且从后向前遍历！

那么本题也是，物品就是 strs 里的字符串，背包容量就是题目描述中的 m 和 n。

代码如下：

```cpp
for (string str : strs) { // 遍历物品
    int oneNum = 0, zeroNum = 0;
    for (char c : str) {
        if (c == '0') zeroNum++;
        else oneNum++;
    }
    for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
        for (int j = n; j >= oneNum; j--) {
            dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
        }
    }
}
```

有同学可能想，那个遍历背包容量的两层 for 循环先后循序有没有什么讲究？

没讲究，都是物品重量的一个维度，先遍历那个都行！

5. 举例推导 dp 数组

以输入：["10","0001","111001","1","0"]，m = 3，n = 3 为例

最后 dp 数组的状态如下所示：

![474.一和零](/media/202106/2021-06-06_221406.png)

以上动规五部曲分析完毕，C++ 代码如下：

```cpp
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
        for (string str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};
```

## 总结

不少同学刷过这道提，可能没有总结这究竟是什么背包。

这道题的本质是有两个维度的 01 背包，如果大家认识到这一点，对这道题的理解就比较深入了。

## 其他语言版本

python:

```python
class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        dp=[[0]*(n+1) for _ in range(m+1)] # 默认初始化0

for item in strs:  # 遍历物品
            zeroNum=0
            oneNum=0
            for i in item:
                if i =='0':
                    zeroNum+=1
                else:
                    oneNum+=1

for i in range(m, zeroNum-1, -1): # 遍历背包容量且从后向前遍历！
                for j in range(n, oneNum-1,-1):
                    dp[i][j]=max(dp[i][j], dp[i-zeroNum][j-oneNum]+1)
        return dp[-1][-1]
```

java:

```java
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][]dp = new int[m+1][n+1];
        for (String str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            char[] charArray = str.toCharArray();
            for (char c : charArray) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
}
```

**如果感觉题解**